|
|
为了实现加工刀具运动的优化控制,本文对数控机床加工优化控制问题进行了研究。首先,基于矢量转接模型,分别建立了折线与直线圆弧段加工优化控制模型;其次,考虑到瞬时启动速度与瞬时启动加速度的存在,对矢量转接模型进行了修正并构建了优化控制修正模型;最后,为了协调加工稳定性与加工效率,借鉴正弦曲线微积分特性,建立了基于正弦函数加减速法的加工优化控制模型。
针对问题一,采用最小偏差插补法作为直线段加工方法,并在矢量转接模型的基础上,分别对折线无误差加工、指定误差加工方式分别进行了分析与建模。在讨论直线段运动阶段划分的前提下,设计了折线加工的通用控制算法流程。以90°与135°折线作为算例,分析了各坐标轴速度变化情况。在转接数上对指定误差优化控制模型进行了改进,将转接数由二次转接推广到了多次转接,建立了多转接加工优化控制模型。
针对问题二,基于圆弧段构成、进给速度、误差限制分析了圆弧段加工的合理方式,并建立了相应的圆弧段加工优化控制模型。考虑到直线圆弧段相切与不相切两种工况,基于指定误差折线加工优化控制模型,进行了直线圆弧段的加工优化控制建模。通过给定的圆角正方形示例对模型及设计算法进行了合理性验证,比较了分别采用S 型加工曲线与非S 型加工曲线的加工效率(用时86.2779s 与84.5036s),结果显示S 型加工曲线效率稍差。
针对问题三,考虑到瞬时启动速度与瞬时启动加速度,对矢量转接模型进行了修正,并将其应用于折线与圆弧段加工优化控制模型中。圆角正方形示例验证结果表明,此时加工效率得到提高(用时81.9055s)。
针对问题四,借鉴正弦曲线微积分特性,提出了基于正弦函数的加减速方法,该方法具有更为统一的构造形式,并保证了加加速度变化的连续性及速度变化的平缓性。基于该加减速方法,以直线段加工为例建立了加工优化控制模型,通过约束加速时间或限制加加速度幅值,可协调加工稳定性与加工效率。
关键词:数控车床;矢量转接;正弦函数;S 型曲线
二、问题分析
本文研究的是工件数控加工控制算法,属于非线性优化问题,涉及立体几何、牛顿力学等内容。
问题一,针对加工型线为折线的加工优化控制问题。影响折线加工效率与精度的因素主要有两方面:1)直线段加工效率与精度;2)转折点转接效率与精度。前者受直线插补算法影响,后者受转接轨迹设计影响且为主要因素。在无误差要求情况下,加工的实际路径必须完全与加工型线一致,当且仅当通过转折处的进给速度降至足够低时才能保证零误差(加工算法误差)。
在有允许误差存在的情况下,实际加工路径可以不经过转折点,进给速度约束有所提升,则有效减少加工时间。在该加工轨迹下,实际加工路径转折点处是由若干段过渡直线段组成,且过渡直线段越多,每次进给速度的偏转角度就越小,偏转时车床能够承受的进给速度就越大,从而减少了转接通过时间,但会导致车床机械损耗及加工成本相应增加。因此在指定加工误差的范围内,优化算法必须能够根据折线夹角的大小选择最优的控制方法,尽少使用过渡直线段[7]。
问题二,针对加工型线为直线圆弧段的加工优化控制问题。影响直线圆弧段加工效率与精度的因素主要有两方面:1)直线段与圆弧段转接效率与精度;2)圆弧段加工效率与精度。对于前者,与问题一有相承接的关系,而后者则受圆弧段半径、弧心角及分段数的影响,是制约直线圆弧段加工效率与精度的重要因素。理论山,当圆弧段所含分接直线段数目越多,则其对转接进给速度的限制则越低,而相应的会增加对机床的机械损耗。因此,在指定加工误差与转接次数限制内,需要建立相应的加工优化控制模型,以实现加工效率与精度的优化目标。
问题三,针对实际加工时存在瞬时启动加速度与瞬时启动速度的加工优化控制问题。实际运动过程中电机启动时允许有一个瞬时启动加速度0 a ,即认为加速度可以从0 瞬间提高到瞬时加速度0 a ,或瞬间从0 a 下降到0,速度也有类似功能。因此,在机床运动轨迹与运动参数可以依托瞬时启动加速度与瞬时启动速度产生更为特殊与灵活的优化设计,从而需要将其纳入问题一与问题二建立的优化控制模型中,使之更为贴近实际工况。
问题四,S 型曲线加工方法在理论上能够提高工件加工过程的平稳性,从而利于避免因启动和停止时速度变化太大引起失步、震荡、超程现象,但同时也会一定程度上降低算法的加工效率。因此需要建立相应的协调控制模型以平衡两者,或在精度与效率的共同约束下,使速度与加速度变化更为平稳,尤其是在电机启动与停止时刻。
三、模型假设及符号说明
3.1 模型假设
假设1:微线段各顶点转接速率不变,即不考虑速率突变。
假设2:忽略直线段自身因插补加工而导致的误差,即认为直线段加工误差相
较于折线与圆弧段加工误差,可以忽略。
假设3:刀头各进给方向最大允许加速度相同,受车床耐受力限制。
3.2 符号说明

四、模型Ⅰ:折线加工优化控制模型
4.1 折线加工建模
4.1.1 直线最小偏差插补法
直线段加工是折线加工的基础,选用最小偏差插补法[9]进行直线段加工。
以二维坐标系为例,设 x_e/y_e 为直线段在xy 坐标轴的分量比。为获得插补最小偏差,对进给方向做如下的规定:
1)当 x_e \geq y_e 时,向x方向或对角线方向(45°方向)中偏差小的方向进给;
2)当 x_e \leq y_e 时,向 y方向或对角线方向中偏差小的方向进给。
以 y=k x(0<k<1) 为例,由于 x_e / y_e=1 / k \text { 且 } 0<k<1 ,则插补方向为x轴方
向或对角线方向中偏差小的方向进给,方向记为 +\Delta x, \quad(+\Delta x,+\Delta y) 。如下图所
示, O\left(x_i, y_i\right) 为插补起始点, A是在 +\Delta x 方向上单步插补后的点,B是x方向上
单步插补后对应的实际轨迹上的点,C是在 \quad(+\Delta x,+\Delta y) 方向上单步插补后的点,
具体如图1 所示。
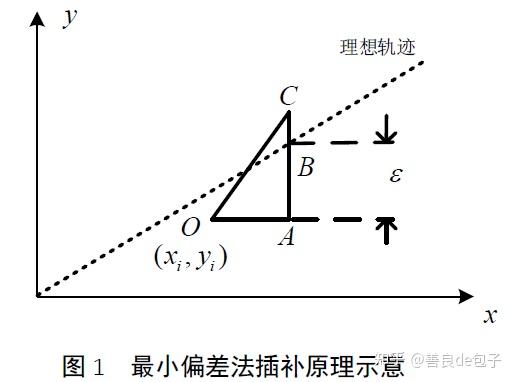
则单步偏差函数为:
\begin{gathered} F(\Delta x)=y_A-y_B=y_i-k\left(x_i+1\right)=\left(x_e y_i-y_e x_i-y_e\right) / x_e \\ F(\Delta x, \Delta y)=y_C-y_B=y_i+1-k\left(x_i+1\right)=\left(x_e y_i-y_e x_i-y_e-x_e\right) / x_e \end{gathered}
由于计算时只关注偏差函数的符号,与数值大小无关,因此,可保留分子部分作为判别式
f=F(\Delta x)+F(\Delta x, \Delta y)=2 F+x_e-y_e
由图可知 F(\Delta x)<0, F(\Delta x, \Delta y)>0, 通过判别函数的符号即可以选择进给 方向。 1) 若 f>0, 则 |F(\Delta x)|<|F(\Delta x, \Delta y)|, 故进给 \Delta x; 2) 若 f \leq 0 则 |F(\Delta x)| \geq|F(\Delta x, \Delta y)|, 故进给 \Delta x, \Delta y 。 此分析方法同样适用于其他象限的分析, 可在揷补过程中的保证偏差最小。
4.1.2 直线段运动阶段划分
对长度L 直线段加工方法进一步讨论,以7 阶段S 型加工曲线加工过程为例,设起始速度与末端速度均为v0,加速度 Jconst ,最大加速度 amax ,如图2所示

则图中, \begin{gathered} s_1=S_7=v_0 \frac{a_{\max }}{J_{\text {const }}}+\frac{a_{\max }^3}{6 J_{\text {const }}^2} \\ s_2=s_6=\frac{a_{\max }\left(V_{\max }-2\right)}{2 J_{\text {const }}}-\frac{a_{\max }^3}{2 J_{\text {const }}^2}+\frac{v_0 V_{\max }}{a_{\max }}+\frac{\left(V_{\max }-\frac{a_{\max }^2}{J_{\text {const }}}\right)^2}{2 a_{\max }} \\ S_3=s_5=\frac{v_{\max }+v_0}{2}\left(\frac{a_{\max }}{J_{\text {const }}}+\frac{V_{\max }}{a_{\max }}\right)-s_1-s_2 \end{gathered}
当 L<2 s_1, 可仅选用加加速与减减速 2 个过程; L<2 s_1+2 s_2 可选用加加速、 匀加速、匀减速与减减速 4 个过程; L<2 s_1+2 s_2+2 s_3 可选用加加速、匀加速、 减加速、加减速、匀减速与减减速 6 个过程; 否则选择完整 7 个过程。
4.1.3 矢量转接模型
对于连续微线段,最大进给速度受相邻线段的夹角限制,对于曲线则受制于曲线的曲率,常因设计者考虑的因素不同而有较大差异。对于折线加工,需要考虑速度约束条件,即具体的空间点上允许的最大进给速度。J.Hu 等设计了矢量转接模型,为目前最广泛应用的微线段转接方法。设定转接前后到头进给速率不变,以机床所能承受的最大加速度在插补周期范围内所允许的最大速度变化量给出连续微线段各顶点处的进给速度满足
2 V_{S e g} \cos (\alpha / 2) \leq A_{\max } \Delta T
则最大进给速度
V_{S e g_{-} \max }=\frac{A_{\max } \Delta T}{2 \cos (\alpha / 2)}
式中, \Delta T 为揷补周期, $\alpha$ 为空间两直线的夹角, A_{\text {max }} 为机床所能承受的最大加 速度, 若取 \Delta T=1 \mathrm{~ms}, A_{\max }=0.6 \mathrm{~m} / \mathrm{s}^2, 则揷补周期内最大速度变化量产生的位 移为 \Delta S=\frac{1}{2} A_{\max } \Delta T^2=3 \times 10^{-4} \mathrm{~mm} \Delta S 一般小于机床控制分辨率,因此, 可对该位移偏移在优化控制中子予以忽 略。
4.1.4 无加工误差控制建模
当顶点进给速度满足式(1)所述速度约束条件时,即
V_{\text {Seg }_{-} o} \leq V_{S e g_{-} \max }=\frac{A_{\max } \Delta T}{2 \cos (\alpha / 2)}
折线加工可以实现无算法误差加工(机床本身加工误差仍存在),为了示意方便,且以xy 二维坐标系统为例,具体如图3 所示。
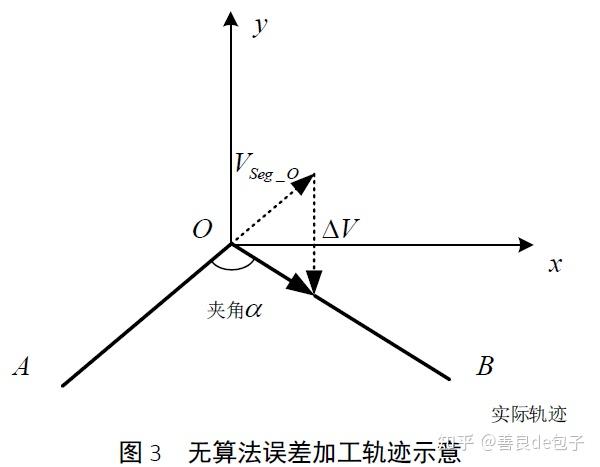
对某折线进行加工, AO = L1, OB= L2 ,若仅考虑匀加速、匀速及匀减速过程,且加速度大小为恒定值,当 L1 , L2 足够大时,刀头进给速率示意如图 4 所示。
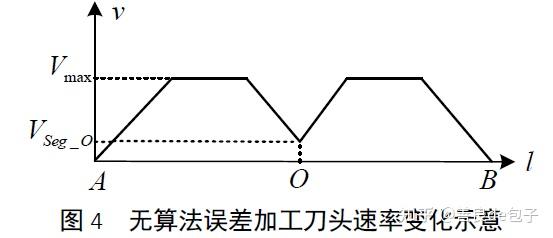
可以发现,在插补周期一定时,机床所能承受的最大加速度是限制无误差(算法误差)转折控制算法效率的关键因素,该控制方式效率较低但具有较高精度。
4.1.5 指定加工误差控制建模
在指定加工误差的条件下,以若干暂态过渡线段代替直接转接方式,能够保证转接的刀头进给速率,既而能在加工误差要求范围内,进可能提高整个工件的加工速率。为了简化分析与加工方便的需要,选择2 次转接,即以一微线段作为暂态过渡,如图5 所示。
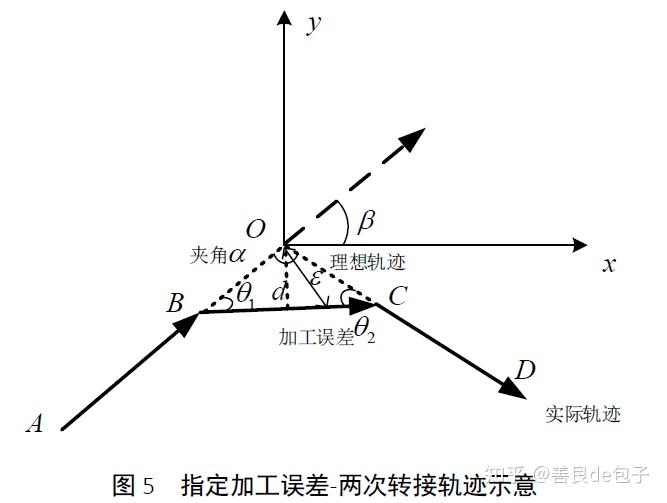
4.2 模型求解与改进
4.2.1 模型求解
取刀具揷补周期 \Delta T=10 m s, 最大进给速度 V_{\max }=0.1 \mathrm{~m} / \mathrm{s}, 最大加速度 a_{\text {max }}=0.6 \mathrm{~m} / \mathrm{s}^2, 指定加工误差 \varepsilon=1 u m, 设两条直线段的长度分别为 L_1=0 . 1m, L_2=0.1 m
1)无误差控制与制定加工误差控制对比
取夹角为90°,其速率变换情况如图7 所示。
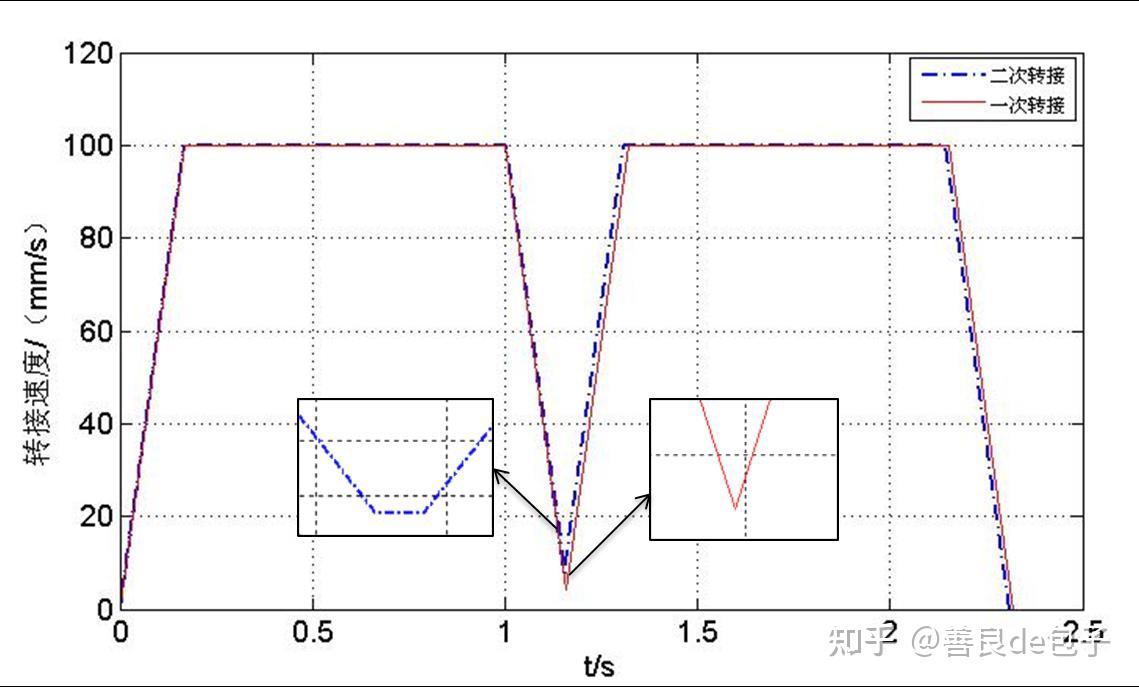
2)90°与135°夹角对进给速度影响对比
分别取折线夹角为90°与135°,其控制算法加工效率如图8 所示。
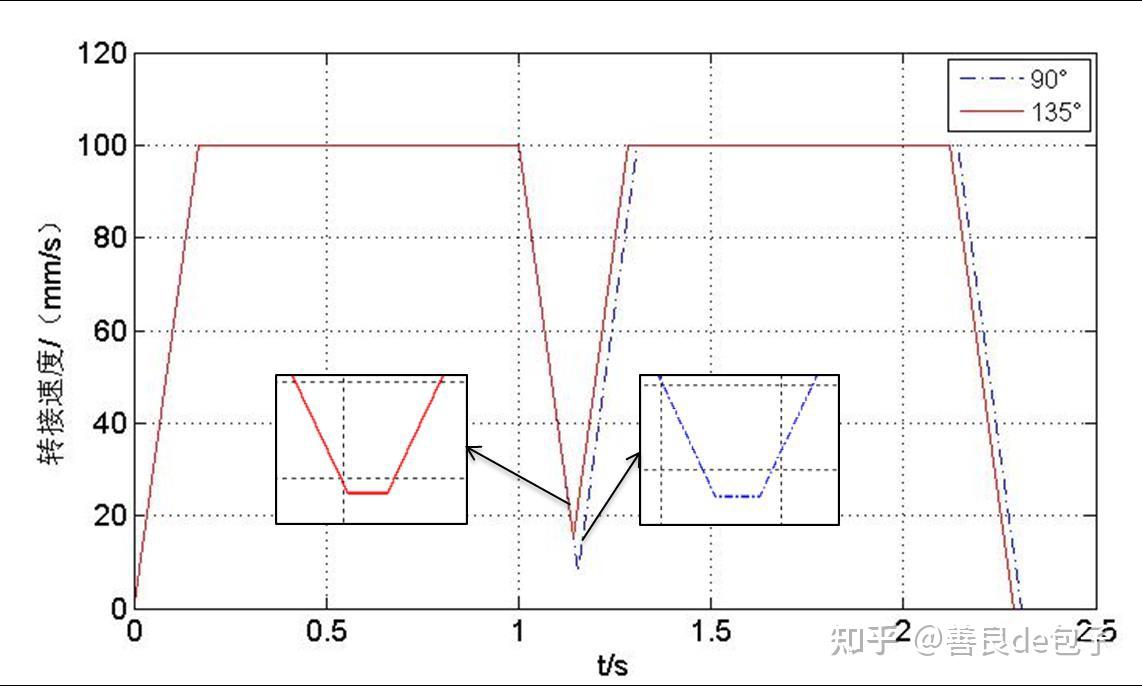
图8 90°与135°转接指定加工误差控制效率对比
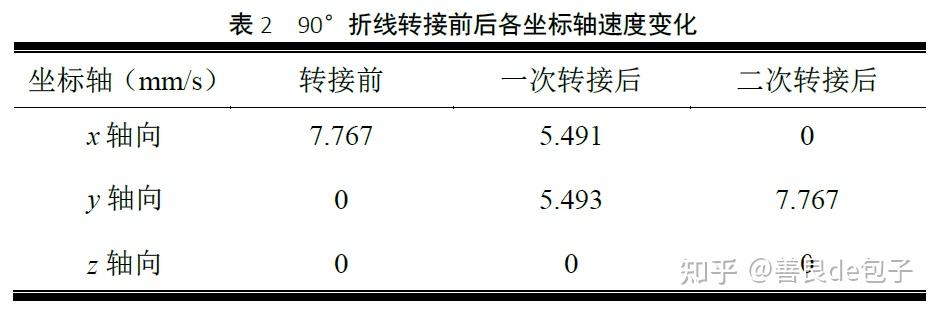
90°折线路径:设各点坐标依次为:A(0,0,0) ,O(100,0,0),D(100,100,0),由优化目标函数求解结果可知,此时转接进给速率vseg=7.767 mm/s,对应两次转接过程 \theta_1= 44.99 , \theta_2= 45.01 。由坐标转换公式可求两次转接前后的坐标速度,具体如表2 所示。
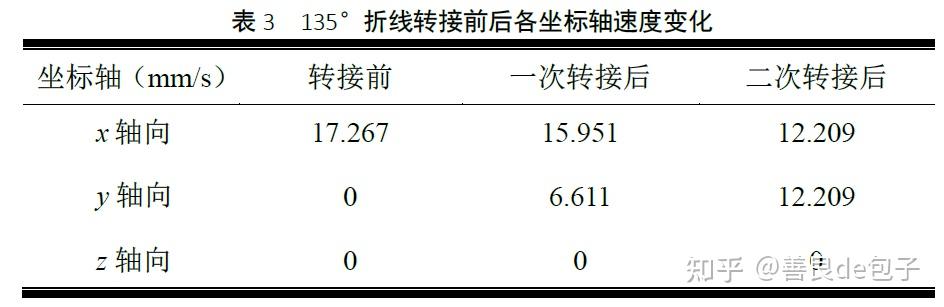
135°折线路径:设各点坐标依次为: A(0,0,0) , O(100,0,0) ,D(170.711,70.711,0) ,由优化目标函数求解结果可知,此时转接进给速率17.267 mm/s ,对应两次转接过程 \theta_1= 22.51 , \theta_2= 22.49 。由坐标转换公式可求两次转接前后的坐标速度,具体如表3 所示。
 |
|